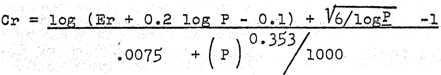Un Molino de bolas de Bond de 12” x 12” esta equipado con un motor eléctrico, reductor de velocidad, contador digital, botón de movimiento para posicionar el cilindro para su carga y descarga, un botón de parada de emergencia, una carga de bolas de 44.5 libras, y una bandeja circular para usar durante el tamizaje.
Se puede usar el molino de Bond del índice de trabajo para calcular el índice de moliendabilidad de Bond.
Las pruebas de moliendabilidad de laboratorio y los resultados comerciales de molienda han mostrado que para muchos materiales el índice de trabajo computado por la siguiente ecuación no permanece constante para diferentes de tamaños de producto P. A medida que P se vuelve más pequeño que los valores Wi pueden disminuir, permanecer constantes, o aumentar. Esto ha sugerido a algunos investigadores que el exponente del producto y tamaños del alimento no permanecen constantes a ½, según se requiera por la Tercera Teoría de Bond, pero puede ser más grande o menor que ½ en casos individuales para producir un índice de trabajo constante. Varias pruebas de moliendabilidad en cada material son necesarias para determinar a este exponente aparentemente variable.
Wi = W/(10/√P – 10√F)
Sin esta variación potencial la Tercera Teoría sobre el índice de trabajo no sería un criterio preciso del trabajo requerido para la reducción de tamaño. En la práctica el índice de trabajo usualmente ha sido determinado en un tamaño del producto cerca del deseado, o han sido determinados en dos o más tamaños del producto y el valor Wi en el deseado tamaño del producto P ha sido encontrado por interpolación. Esto ha resultado ser muy satisfactorio, excepto que la cantidad de pruebas de laboratorios requerido ha aumentado. Una mejor comprensión del proceso de conminución debería revelar las razones para las variaciones del índice de trabajo en los tamaños diferentes del producto, y debería hacer posibles más cálculos precisos de molienda sin aumentar el número de pruebas del grindability requeridas.
La ecuación básica del índice de trabajo es:
W = 10 Wi/√P – 10 Wi/√F
Recientemente ha sido mostrado que para cualquier material energía alimentada permanece sustancialmente constante para cada unidad de una nueva grieta producida cuando se hace la molienda para tamaños diferentes de producto, si bien los valores del índice de trabajo variaron ampliamente. Esto confirma la Tercera Teoría y sugiere que el trabajo en el que las variaciones del índice están causadas por variaciones en distribuciones finas del tamaño del alimento y producto. Estas distribuciones finas de tamaño no son indicadas por los tamaños del 80 % pasante usado en la ecuación anterior y llamadas como F y P. El uso del tamaño del 80 % pasante como el criterio exclusivo de tamaño de la partícula asume que el alimento chancado o molido y el producto siguen una distribución de tamaño consistente. Cualquier variación de estos valores promedios de alimento o producto causará que el índice de trabajo aumenta o disminuye con molienda más fina.
Las variaciones en la tercera teoría para el índice de trabajo moliendo el mismo material para tamaños de productos diferentes están causadas por diferencias en la relación de la proporción de exposición del alimento a la proporción del producto. La proporción de exposición es una medida de la cantidad de presente de finos, y es encontrada de un gráfico de un análisis de tamaño en papel semilogarítmico.
Las ecuaciones se dan por los valores del índice de trabajo en los tamaños diferentes del producto y pueden calcularse de los resultados de una prueba de laboratorio o molienda comercial, y los ratios de exposición de alimento y producto. Estos valores calculados pueden ser comprobados por mediciones de molienda en otros tamaños del producto. Las ecuaciones son incluidas para el cálculo de la energía de la grieta de específica longitud y de la grieta. La relación entre el índice de trabajo y la longitud de la grieta producida son mostradas. La ecuación es dada para usar los valores calculados del índice de trabajo del alimento y producto para obtener más valores precisos del trabajo requerido.
La siguiente ecuación puede usarse para calcular la longitud de la grieta.
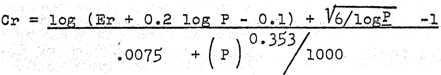
La información de plantas o las pruebas de planta piloto pueden demostrar que la proporción Erf/Erp es diferente en la planta que en las pruebas de moliendabilidad de laboratorio. En este caso la proporción de planta debería ser usada con el índice de trabajo estándar calculado debe ser similar con el índice de trabajo de la planta según la ecuación:
Wip = Wi100 + (p – 100) (.018 – .014 Erf/Erp)
La aplicación de las ecuaciones muestra que la causa principal de variaciones del índice de trabajo en los diferentes tamaños del producto es la diferencia en la distribución de tamaño del alimento y el producto, y que la Tercera Teoría sobre el Índice de Trabajo permanece constante cuando estos son tomados en consideración. Mucho debe hacerse en explicar por qué ciertos materiales se quiebran para formar diferentes cantidades de finos, y por qué los valores Er de ciertos materiales puede diferir ampliamente en los tamaños del alimento y del producto, así como también el efecto de tamaños de grano en los valores Er. La necesidad de más estudios a lo largo de esta línea es evidente.
El índice de trabajo Wi como se determinó previamente a un 80% pasante del producto es todavía el criterio más práctico del trabajo requerido para que la reducción se acerque a ese tamaño. La medición de las proporciones de exposición del alimento y producto puede aumentar la exactitud de cálculos de aporte de trabajo en los tamaños del alimento y el producto de esas pruebas.
Indice de Trabajo Promedio para un Molino de Barras y un Molino de Bolas
Copyright 2012-2024 911Metallurgist | All Rights Reserved
